Normed Division Algebra Over The Real Numbers

01 Mar, 2021

Every real normed division algebra is isomorphic to the set of all real numbers R the complex numbers C or the quaternions H. Theorem 12 Complex Version.

Algebra Paper Retracted Because Of Questions About The Integrity Of The Mathematics Retraction Watch

The real numbers the complex numbers the quaternions and the octonions.

Normed division algebra over the real numbers. R 4 ostrictly real type i -x 2 is quasiregularor every x. R 2 iA does not contain any subalgebra ocomplex type with identity. Its generated by elements of some inner product vector space I subject to relations v 2 v v.

Indeed these three choices appear naturally in a number of axiomatic approaches. The real numbers the complex numbers and the quaternions. Here x c a r d i N.

X i 0. Essentially one first proves that any real division algebra D is a Clifford algebra ie. In this case an x are the approximation numbers of the sequence x a n x inf x x.

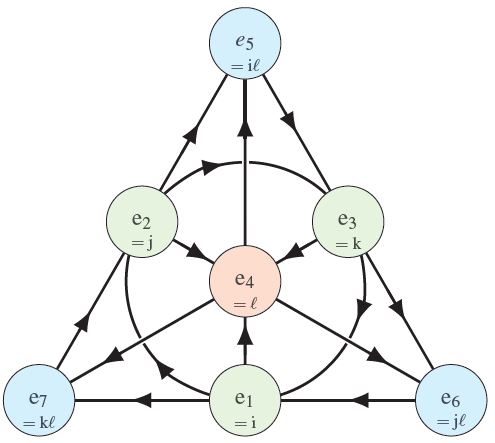
C a r d x n. Let ℓ be the normed algebra 1 of all bounded sequences real or complex numbers with x sup n x n. First one splits D as R D 0 where D 0 is the space of elements with T r 0 and then one observes that minimal polynomial of a traceless element has the form x 2 a 0 its quadratic because.

The Hurwitz theorem says that over the real numbers there are up to isomorphism exactly four finite-dimensonal normed division algebras. The property of having a norm compatible with multiplication essentially expresses that your division algebra is very similar to the real numbers where the ordinary absolute value is such a norm There doesnt seem to be a reason this property should extend to more exotic algebras. With this guarantee of an additive and multiplicative inverse we are able to subtract and multiply elements as well as add and multiply them and thus we do indeed have a normed division algebra.

By the Hurwitz theorem these are the real numbers complex numbers quaternions and octonions. The real numbers R the complex numbers C the quaternions H and the octonions O. For many applications also to physics the most interesting division algebras are the normed division algebras over the real numbers.

Exceptional spinors and real normed division algebras. Also note that the multiplicative inverse of z 2Cz 6 0 is z 1 z jjzjj2 a. Hurwitzs theoremsays that there are only 4 normed division algebras over the real numbers up to isomorphism.

A division algebra over the real numbers R is a division ring that has the reals as a subfield. The proof was published in 1923. There are only four finite-dimensional normed division algebras.

De nition Real Division Algebra Let A eb an algebra over R not on-c taining only of its zero-element. 2 Nature admits only four NDAs over the reals.

There are precisely four normed division algebras. Over the complex numbers the only normed division algebra is the algebra of complex numbers themselves. This was proved by Hurwitz in 1898.

These have important relations to supersymmetry. Its a famous result and several other proofs are known. B a2 b20.

A normed division algebra NDA is a division algebra where in addition a b a b. Theorem 11 Real Version. A real normed algebra A is said to be.

Starting from the real numbers and generalizing to the complex numbers one has to give up the ordered property of the reals. Frobenius proved in 1877 that the only division algebras over R of finite dimension are a R itself of dimension 1 b the complex numbers C a field of dimension 2 over R and c the quaternions H a skew field of dimension 4 over R. We say that C is a normed division algebra.

The problem of real division algebra is to show that there. The generic term isonion although the term includes other algebras such as the sedenions. Ive spent a lot of time studying them.

R1 oreal type i A is not ocomplex type. The reals themselves R the complex numbers C the quaternions H and the octonions O. A is a aler division algebra if for any a A and any non-zero b A there exists exactly on x and y in A such that a bx and a yb This de nition does not assume that the algebra A is either commutative or as-sociative.

However there are internal problems with real or quaternionic quantum theory. Adolf Hurwitz Über die Composition der quadratischen Formen von beliebig vielen Variabeln Nachr. Baez Quantum theory may be formulated using Hilbert spaces over any of the three associative normed division algebras.

Every complex normed division algebra is isometrically isomorphic to C. The wikipedia page on division algebras mentions that any finite-dimensional division algebra over the reals must be of dimension 1 2 4 or 8. The division algebra H of quaternions is the algebra consisting of elements of form x 01.

It also mentions the only finite-dimensional division algebras over the real numbers which are alternative algebras are the real numbers themselves the complex numbers the quaternions and the octonions. The real numbers the complex numbers the quaternions and the octonions.

Https Arxiv Org Pdf 1603 00681

Division Algebras And Supersymmetry Ii The N Category Cafe

Why Can T A Normed Division Algebra Be Of 3 Dimensions Quora

Https Projecteuclid Org Download Pdf 1 Euclid Jgsp 1548471826

Pdf The Octonions

Octonions Exceptional Jordan Algebra And The Role Of The Group F4 In Particle Physics Request Pdf

Http Www Worldscientific Com Doi Pdfplus 10 1142 S0129055x17500118 Src Recsys

Https Www E Periodica Ch Cntmng Pid Ens 001 1980 26 25

John Carlos Baez On Twitter Take The Real Numbers Throw In Some Square Roots Of 1 And Some Square Roots Of 1 All Anticommuting You Get A Clifford Algebra Clifford Algebras Are

Normed Division Algebra In Nlab

Pdf The Classification Of Real Division Algebras

Braids Normed Division Algebras And Standard Model Symmetries Sciencedirect

Division Algebras Poincare Conjecture Correspondence Topic Of Research Paper In Physical Sciences Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub